Introduction
D-Pad, analog stick, joystick. If you are developing a game, at one point you have to deal with analog inputs from a controller. A common problem with these analog inputs is that most don’t return a rest state value (typically 0) when they are in their rest state. There could be various reasons for it. From the analog input not centered to it exhibit hysteresis by returning a slight more negative or positive value depending on the last input.
Deadband
The simplest method is to reject any input unless it is above a certain value. This technique has multiple names: deadband, dead zone or notch filtering. In the C++ code below it checks if the absolute value of the input (assumed to ranged between [-1,1]) is less than the deadband cutoff. If the joystick value is below the cutoff, the code returns 0 (which is the rest state). Otherwise it returns the value of the input.
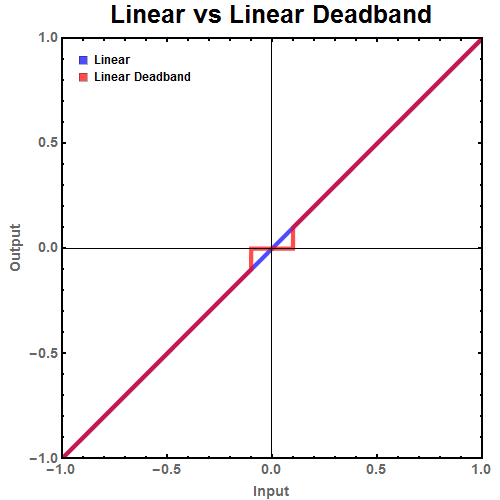
Figure 1: Ideal linear behavior of a joystick compared to the behavior of the joystick with a deadband.
While this deadband does solve the issue by returning the rest state value even when the analog controller reports a small positive or negative value, it creates a new problem. As you can see in Figure 1, the deadband has created a jump in the values. Small movements have essentially been cut out. The remaining input needs to be scaled so that the small values are still accessible.
Linear Scaled Deadband
In order to eliminate the jump present in the deadband, there needs to be a function that maps the remaining input to the full range of [-1,1]. Using the equation below any continuous odd function, \(f(x)\), can be used to map the input to the output and eliminate the jump.
- \(x\) is the analog input which ranges from [-1,1].
- \(ScaledDB(x)\) is the deadband scaled equation.
- \(f(x)\) is the non-deadband function that maps analog input to output.
- \(Sign(x)\) returns -1,0,+1 depending on the sign of the input.
- \(max f(x)\) is the maximum value of \(f(x)\).
- \(DB\) is half the total deadband size.
While the above equation looks complicated in practice it reduces to something very simple.
Replacing:
- \(f(x)\) with a linear equation \(f(x)=x\).
- \(Sign(x)\) with \(\frac{Abs[x]}{x}\)
- \(max f(x)\) with 1 since our data ranges from [-1,1].
- \(DB\) with 0.1 which I arbitrarily picked so the deadband goes from (-0.1,0.1).
Reduces to the equation:
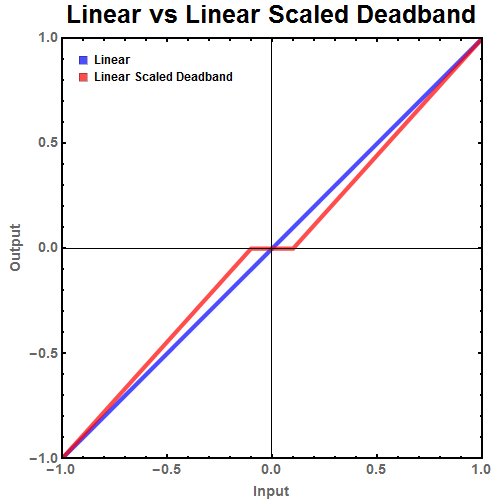 Figure 2: Ideal linear behavior of a joystick compared to the behavior of the joystick with a linear scaled deadband. Full range of output is now preserved.
Figure 2: Ideal linear behavior of a joystick compared to the behavior of the joystick with a linear scaled deadband. Full range of output is now preserved.
Figure 2 shows that the linear scaled deadband has eliminated the jump at a small cost of precision. While this now falls in line with the users expected behavior, is there a way to further improve this?
Cubic Scaled Deadband
The previous equation traded precision in order to eliminate the issue of the input not centering correctly. Is there a way to gain some of the precision back? In a way yes. For most analog inputs, like a car’s gas pedal, small changes to small values matter more than small changes to large values. For example going 5 mph faster then intended is much more serious when parking a car than when one is driving on the freeway.
With that in mind, the linear equation used to map input to output can be replaced with another equation that gives more precision at lower values. The equation below is one such replacement for the linear equation \(f(x) = x\):
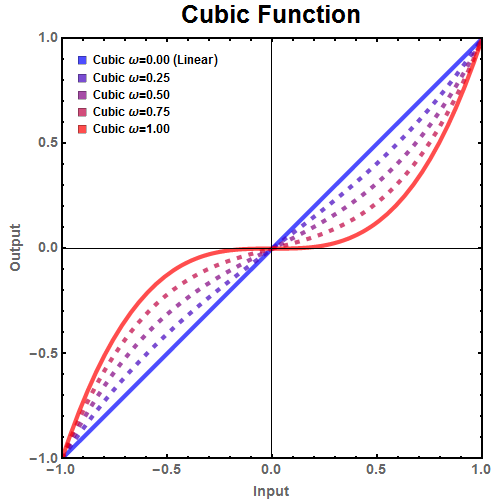 Figure 3: Plot of a potential replacement for the linear scaling function, the cubic function. \(\omega\) can control how much precision is allocated to smaller movements.
Figure 3: Plot of a potential replacement for the linear scaling function, the cubic function. \(\omega\) can control how much precision is allocated to smaller movements.
As seen in the Figure 3, increasing the weight, \(\omega\), increase the sensitivity at lower input values while decreasing the sensitivity at higher values. This function can be used in the scaled deadband function, \(ScaledDB\), to produce a cubic scaled deadband.
Inserting \(f_{Cubic}(x,\omega)\) into \(ScaledDB\) results in the following equation:
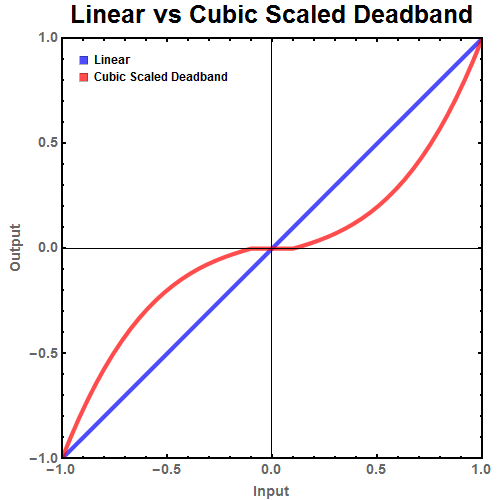 Figure 4: Ideal linear behavior of a joystick compared to the behavior of the joystick with a cubic scaled deadband. Precision is increased at lower values for the input at the cost of lower precision at higher values.
Figure 4: Ideal linear behavior of a joystick compared to the behavior of the joystick with a cubic scaled deadband. Precision is increased at lower values for the input at the cost of lower precision at higher values.
Conclusion
Deadbands are a common technique to sanitized joystick input and eliminate erroneous input. While simple to implement, the loss of small precises movement needs to be accounted for. By using a cubic scaled deadband, erroneous input can be suppressed while increasing the precision of small movements.